微积分马上就要结课了，然后感觉级数这一块还是得总结一下
$8.1级数的定义和性质
第一个重要概念：级数的概念(什么是级数) 个人理解，级数就是一列无限项的数列比如u1,u2,u3,u4....un....，其中为un为级数的一般项，相当于数列里面的通项。 第二个重要概念：级数的部分和(记为Sn) Sn=u1+u2+u3+u4....+un,其实类似数列的前n项和 最最最重要的概念：级数的收敛和发散（这个不知道后面都不用学了） 如果limn->∞Sn存在，值记为S，那么称级数∑un收敛，且称级数的和为S。(在级数可以隔项相消的时候很有用！) 同理，如果limn->∞Sn不存在，则称级数∑un发散。 书上还有个余项的概念，我没怎么在意，感觉和泰勒公式里面的余项类似，就是一种理想结果和实际的差值的绝对值。 自己随意地理解一下就ok了。 好的，了解了什么是级数之后，8.1的后面介绍了几种级数的性质(随意看下，结合定义理解起来很简单所以我说一定要弄清楚级数收敛的定义) 性质一： 如果级数∑un收敛，和记为S，那么级数∑kun也收敛且和为kS，k为常数。 性质二： 如果级数∑un和级数∑vn均收敛，和分别为p和q，那么级数∑(un±vn)也收敛，且和为p±q。 性质三： 级数前面减去或者加上有限项并不改变级数的敛散性，但在级数收敛的时候，一般会改变级数的和。 性质四： 如果一个级数收敛，那么加括号后的级数也收敛。反之不一定成立！反之不一定成立！反之不一定成立！ 性质随意看一下就ok，定义要好好理解，8.1大概就是这些了。 最最最最最最后一点，级数收敛的必要条件：当n->∞时,un=0，这就是说你以后看见一个级数，先看一眼一般项的极限就可以初步判断级数收敛的可能了，所以这个还是很重要的
$8.2常数项级数的判别法
首先不得不说这一节非常重要，非常重要，做个标记，非常重要，常数项级数一般就是考的这个了，其他可能会涉及到后面的幂级数，这个后面再说。
一、正项级数判敛(正项级数就是一般项un≥0的级数)
定理一：充要条件！
设∑un为正项级数，那么∑un收敛的充要条件是它的部分和数列有界(证明用极限里面的单调有界准则，很简单)
定理二：比较判敛法 通俗一点讲就是，
如果一个正项级数∑un的一般项小于一个收敛正项级数的一般项，则级数∑un收敛
如果一个正项级数∑un的一般项大于一个发散正项级数的一般项，则级数∑un发散
随意理解一下就ok，这个用习惯了很好想。
然后这里提出一个p级数的版子，挺重要的。
级数∑1/np被成为p级数(p>0)，它有下面特点
当p≤1的时候，p级数发散
当p>1的时候，p级数收敛
定理三：一般项等价，级数同敛散
设∑un和∑vn都是正项级数，如果两级数的一般项在n趋于无穷的时候为同阶无穷小，那么两级数同时收敛或发散。
比如下面这道题.... 
一开始我拿到这个题一直想用比较判敛法，但是总是判断不出来，后来听老师讲了之后才知道有这个方法.....
这道题只要把级数取绝对值直接去证绝对收敛就ok，把其一般项和n*(1/n)a2n做比值然后取极限就ok，然后因为tanx和x在
x趋于0的时候是等价无穷小，所以原级数取绝对值后和∑a2n同敛散所以其绝对收敛
定理四：比值判敛法(达朗贝尔判别法)
即用limn->∞un+1/un=ρ(0≤ρ≤+∞)来判断级数的敛散性 ρ<1时，级数∑un收敛
ρ>1时，级数∑un发散 ρ=1时，无法判断。
这个方法也挺重要的，而且在后面幂级数的敛散判断里面也有推论，多看看也不是很难掌握。
定理五：根值判敛法(柯西判敛法)
也即把级数一般项开n次方然后取n->∞的极限来判断敛散性
设极限为ρ，那么同样有 ρ<1时，级数∑un收敛 ρ>1时，级数∑un发散
ρ=1时，无法判断。
到这里正项级数的判敛方法就讲完了！这个很重要，要多看
二、交错级数的判敛法
什么是交错级数？ 交错级数就是 ∑(-1)n-1un或∑(-1)nun这种的级数
其收敛必须具备两个条件
1、满足级数收敛的通用必要条件->当一般项的n->∞的时候极限为0
2、级数的un单调不增。 这里有个经典的利用这个结论的题目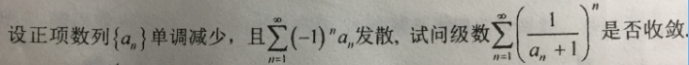 
这里正项级数an单调减少，但是交错级数却发散，所以an最后不是趋近于0而是趋于一个正数。之后再用柯西判敛法，取个1/n次方之后1/(an+1)小于1，所以该最后得出结论，题中级数收敛。
其他的题目感觉就是硬套结论没什么好说的。
三、绝对收敛和条件收敛
这一部分一开始就拿出一个结论：
定理7：如果一个级数的绝对值级数(绝对值级数就是把某个级数的一般项取绝对值后得到的级数)收敛，那么它的原级数也收敛。
这个结论非常非常的有用，它可以把一个任意级数转为判断正项级数，这样就可以使用正项级数判敛法了。
顺便在这里提出一个常用范例：级数∑1/n和∑(-1)n-1(1/n),这里前者是发散的，后者是收敛的，这个结论蛮常用的。
后面介绍了一个定义：如果一个级数它的绝对值级数收敛，那么称这个级数绝对收敛，如果一个级数的绝对值级数发散，而级数自身收敛，那么称这个级数条件收敛。
这个定义没啥用，只是用来做题和称呼。
Tips:在有了条件收敛和绝对收敛之后，判断一个非正项级数的敛散性的时候就一定要说明是绝对收敛还是条件收敛了。
条件收敛的定理8，9我觉得不是很重要(起码暂时还不觉得.....),所以我就简单的列出来吧，大家看下就可以了。
定理8：绝对收敛级数不因为改变项的位置而改变它的和
定理9：设级数∑un和∑vn都是绝对收敛的，其和分别为S和σ，那么它们的柯西乘积
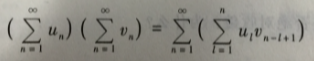也绝对收敛，且和为S+σ。
$8.3幂级数
非常非常非常重要的一节，可以说是级数一章的灵魂了
首先函数项级数的定义:
给定一个区间I上定义的函数列，u1(x),u2(x),u3(x)....un(x)....,则由该函数列所构成的表达式∑un(x)就是定义在∑un区间I上的函数项级数。
说白了就是把级数的项改成和x有关的函数，构成的级数就是函数项级数。
然后定义二是关于收敛点的，就是在某个定义域内部的点x0，如果∑un(x0)收敛，那么称x0为级数的收敛点，如果发散就是发散点；全体收敛点的集合称为函数项级数的收敛域。
上面所有和定义域相关的东西都重点标记了，以后在函数项级数里面，所有的结果，都必须带上相应的域，否则算结果不完整！
然后到幂级数
定义：形如∑anxn=a0+a1x+a2x2+...anxn...的函数项级数称为幂级数，其中a0，a1，a2...an被称为幂级数的系数。
简单易懂，就是函数项都为幂函数的级数就是幂级数 然后一个不起眼的重要结论
定理一->阿贝尔定理:
如果幂级数在点x0处收敛，那么当x<x0的时候幂级数也收敛
如果幂级数在点x0处发散，那么当x>x0的时候幂级数也发散
下面定理二，这个真的很重要很重要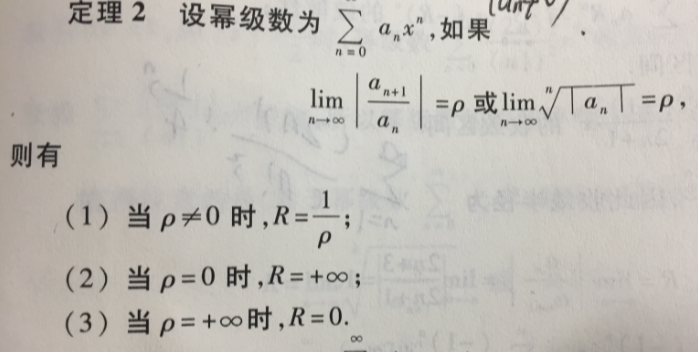 
其中这个R是收敛半径，也就是说级数在(-R,R),[-R,R),(-R,R]或[-R,R]上面收敛。两个端点要靠带进去来判断。
有了这个结论，几乎所有的题目都是n+1项比第n项，看收敛半径，如果有n次方的话，那就开个n次方，然后依旧得出收敛区间
幂级数的加减一块我觉得不是很重要，此处省略。。。 和函数的性质，这个直接涉及到了幂级数求和了....幂级数求和主要涉及三个方法 第一个：连续->幂级数的收敛区间的端点如果收敛，那么其和函数就在这一点连续。 第二个：求导->简单点说就是幂级数的和函数可以由该级数的一般项求导后求和，然后对结果积分算出来。 第三个：积分->同二，就是可以先积分再求和最后再对结果求导得出和函数。 这三个结论用的熟不熟，直接决定了能不能正确的求出幂级数的和函数！需要多加练习。